Пилипчук О. П., вчитель фізики та інформатики Гаврилівської ЗОШ І-ІІІ ступенів Теофіпольського району Хмельницької області
Задача про розрізання квадрата (ООП, Python 3)
В шкільних програмах з інформатики останніх років з’явилось поняття “об’єктно-орієнтоване програмування”. Проте для багатьох вчителів, що мають досвід викладання учням основ процедурного програмування, виявляється складно перебудувати виклад так, щоб охопити обидві парадигми.
Спробую проілюструвати, як об’єктноорієнтований підхід можна використати під час розв’язування задачі, що пропонувалась на Хмельницькій обласній Інтернет-олімпіаді 2019 року.
Задача
Клаптики. Квадрат, дві сторони якого лежать на координатних осях у першому координатному куті, розрізали в довільному місці по вертикалі або по горизонталі. Після цього з отриманими частинами 0 або більше разів виконали подібну операцію. Яка площа найбільшого клаптика?
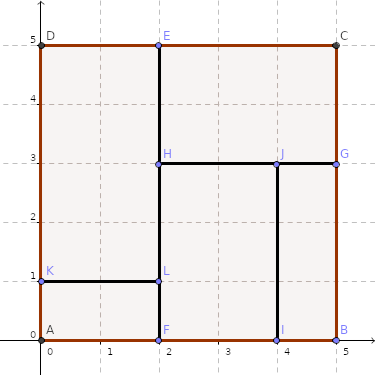
Вхідні дані. У першому рядку стандартного вхідного потоку записано два цілі числа, відокремлені пропуском, — довжина сторони квадрата L і кількість розрізів N. У наступних N рядках записано по 4 цілі числа x1i, y1i, x2i, y2i, відокремлені пропусками,— координати кінців i-го розрізу. Розрізи перелічені в довільному порядку.
Вихідні дані. У стандартний вихідний потік вивести одне ціле число — найбільшу площу клаптика.
| Зразок вхідних даних |
Зразок вихідних даних |
5 4
0 1 2 1
2 3 5 3
2 0 2 5
4 3 4 0 |
8 |
Ідея
Спочатку ми маємо один квадратний клаптик:

і певний набір відрізків, які далі називатимемо розрізами:

Переглядатимемо список розрізів, перевіряючи щоразу, чи не можна черговим з них розрізати квадрат. Таким чином, зупинимось на третьому розрізі, який розділить початковий клаптик на 2 менші:

А невикористаних розрізів стало на один менше:

Подальший алгоритм дій такий:
Доки не закінчились розрізи, для кожного з клаптиків шукати, чи не можна його розрізати; якщо можна — відрізаний клаптик додати до всіх, а розріз вилучити. Після цього вивести найбільшу площу клаптика.
Мовою Python це може виглядати так (основна частина):
while len(RList)>0: |
# Поки список розрізів RList не порожній...
|
for KL in KList: |
#... для кожного клаптика KL зі списку клаптиків KList...
|
for RZ in RList: |
#... перебирати розрізи в списку RList і...
|
if KL.rizaty(RZ,KList): |
#... якщо поточний розріз RZ підходить до клаптика KL,...
#... то розрізати його, відрізаний клаптик додати до KList,...
|
RList.remove(RZ) |
#... вилучити RZ зі списку розрізів...
|
break |
#... і перейти до наступного клаптика.
|
Примітка. Описаний алгоритм можна покращити. Якщо під час перевірки чергового клаптика KL для нього не знайшлося жодного розрізу RZ, то:
- його варто вилучити зі списку KList - це прискорить подальшу роботу;
- перед вилученням слід запам'ятати його площу, оскільки вона може виявитися шуканою найбільшою площею.
Пропоную читачам виконати це вдосконалення програми самостійно.
Звичайно, програма запрацює, тільки якщо належним чином описати класи об’єктів і забезпечити введення та виведення даних, тому розглянемо повний її текст. Програма перевірена в середовищі програмування IDLE мовою програмування Python версії 3.7.5.
Програма
Якщо з подальшого тексту вилучити нумеровані коментарі, отримаємо працездатну програму (принаймні, так було задумано :).
1. Описуємо клас Rozriz. Він має лише метод-конструктор “Створення примірника класу Rozriz”:
class Rozriz:
def __init__(self,x1,y1,x2,y2): # створюється за 4 числами - координатами кінців
self.x1=min(x1,x2)
self.y1=min(y1,y2)
self.x2=max(x1,x2)
self.y2=max(y1,y2)
2. Описуємо клас Klaptik. Реалізуємо метод-конструктор “Створення примірника класу Klaptik”:
class Klaptik:
def __init__(self,x1,y1,x2,y2): # створюється за 4 числами - координатами двох протилежних кутів
self.x1=x1
self.y1=y1
self.x2=x2
self.y2=y2
3. Реалізуємо метод “Розрізання клаптика”. Вхідними параметрами для нього є розріз R і список K, до якого слід додати відрізаний клаптик:
def rizaty(self,R,K):
rez=False # змінна-прапорець “Чи вдалось розрізати?”
# перевіряємо, чи підходить розріз до цього клаптика.
# ГОРИЗОНТАЛЬНИЙ розріз?
if (R.x1==self.x1) and (R.x2==self.x2) and (R.y1>self.y1) and (R.y1<self.y2):
# додаємо до K відрізаний клаптик
K.append(Klaptik(self.x1,self.y1,self.x2,R.y2))
# зменшуємо клаптик, який різали
self.y1=R.y1
# встановлюємо прапорець “Відрізано”
rez=True
# ВЕРТИКАЛЬНИЙ розріз?
elif (R.y1==self.y1) and (R.y2==self.y2) and (R.x1>self.x1) and (R.x1<self.x2):
K.append(Klaptik(self.x1,self.y1,R.x2,self.y2))
self.x1=R.x1
rez=True
# повідомляємо на місце виклику, чи вдалось розрізати
return(rez)
4. Вводимо дані:
L,N=map(int,input().split())
# Створюємо порожній список для клаптиків...
KList=[]
#...і додаємо до нього початковий квадрат.
KList.append(Klaptik(0,0,L,L))
# Створюємо порожній список для розрізів...
RList=[]
for i in range(N):
#... вводимо координати кінців чергового розрізу...
x1,y1,x2,y2=map(int,input().split())
#... і додаємо до списку розрізів.
RList.append(Rozriz(x1,y1,x2,y2));
5. Реалізуємо розглянутий вище алгоритм:
while len(RList)>0:
for RZ in RList:
for KL in KList:
if KL.rizaty(RZ,KList):
RList.remove(RZ)
break
6. Знаходимо в списку клаптик з найбільшою площею:
S=0
for KL in KList:
S=max(S,(KL.x2-KL.x1)*(KL.y2-KL.y1))
7. Виводимо результат :) :
print(S)
Перегляньте також розбір цієї ж задачі, проілюстрований мовами Pascal і C#.
Интернет реклама










